O pesadelo do arredondamento nos projetos de migração

Migrar sistemas de uma plataforma para outra nos coloca diante de desafios às vezes bem maiores do que ter que tomar decisões de infraestrutura e arquitetura de aplicação.

E um deles, com certeza, está nos diferentes critérios de arredondamento de valores com casas decimais.

A expectativa

Vamos supor que alguém tenha decidido reescrever em Java um sistema financeiro originalmente desenvolvido em COBOL. Sabemos de antemão que esse é um sistema de cálculo intensivo, e na fase de planejamento e decisões de arquitetura imaginamos que teremos que lidar com coisas assim:

identification division.
program-id. gtc027.
data division.
working-storage section.
01 x0 pic 9(005)v9(006) comp-3 value 7268.35.
01 x1 pic 9(005)v9(006) comp-3 value zeros.
procedure division.
   compute x1 = x0 / 2
   display "X1=" x1.
   stop run.

Que ao ser executado exibe esse resultado…

X1=03634.175000

Então imediatamente visualizamos que a versão convertida desse programa ficaria assim…

public class Jgtc002 {
    public static void main(String[] args) throws Exception {
        double x0 = 7268.35;
        double x1 = 0;
        x1 = x0 / 2;
        System.out.println("X1=" + String.format("%5.6f", x1));
        System.exit(0);
    }
}

…e que o resultado seria esse…

X1=3634.175000

– “Cadê o problema? Deixa de ser pessimista, cara!”

Aí vem a realidade

Começa o projeto e começam chegar os programas de verdade: milhares de programas que processam milhões de transações por dia com dezenas de cálculos bem mais complexos para cada transação.

Para demonstrar a dificuldade, vou usar um problema que ficou conhecido como Muller’s Recurrence, elaborado por um professor de ciência da computação na França chamado Jean-Michel Muller, que faz pesquisas na área de confiabilidade e precisão de sistemas.

O problema proposto por Muller é matematicamente simples: apenas subtrações e divisões num loop que se repete uma determinada quantidade de vezes:

x0 = 4
x1 = 4.25
x2 = f(x1, x0)
x3 = f(x2, x1)
...
xn = f(xn-1, xn-2)

f(y, z) = 108 - ((815 - (1500 / z)) / y)

Para fazer essa experiência, codifiquei o programa abaixo no mainframe…

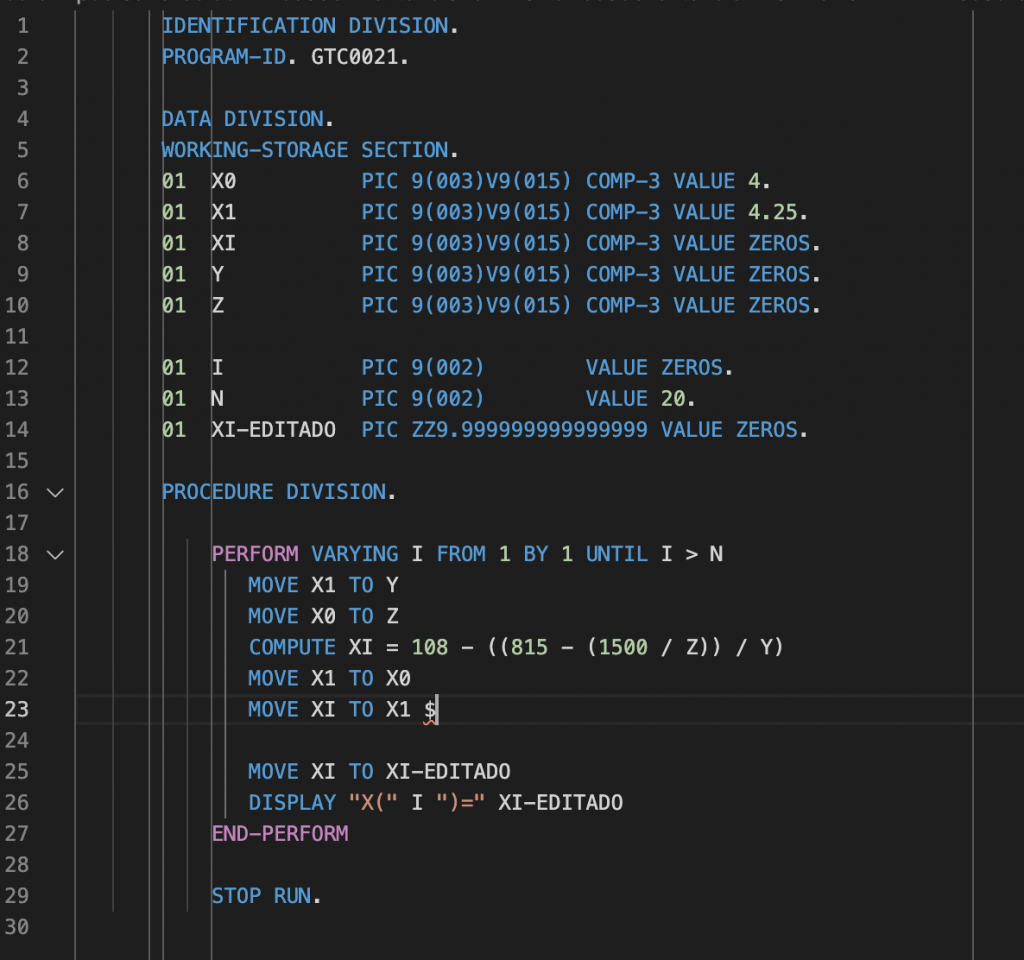
…compilei com o IBM Enterprise COBOL for Z…

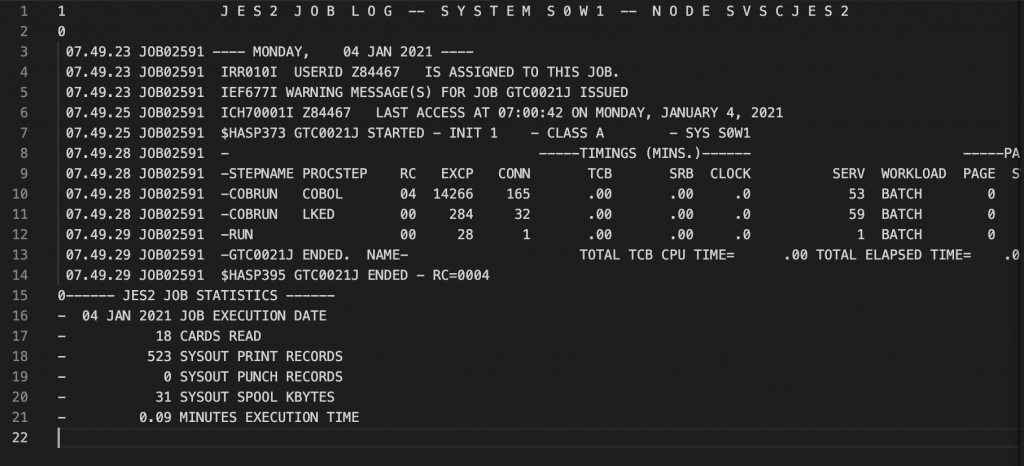
Executei esse mesmo programa em plataforma Linux, usando o GnuCOBOL como compilador e usei a diretiva -std=ibm para garantir que os critérios de arredondamento seriam iguais aos do mainframe. O resultado foi idêntico até na warning da compilação:

Em COBOL no Mainframe:
X(01)=  4.470588235294118
X(02)=  4.644736842105272
X(03)=  4.770538243626253
X(04)=  4.855700712593068
X(05)=  4.910847499165008
X(06)=  4.945537405797454
X(07)=  4.966962615594416
X(08)=  4.980046382396752
X(09)=  4.987993122733704
X(10)=  4.993044417666328
X(11)=  5.001145954388894
X(12)=  5.107165361144283
X(13)=  7.147823677868234
X(14)= 35.069409660592417
X(15)= 90.744337001124836
X(16)= 99.490073035205414
X(17)= 99.974374743980031
X(18)= 99.998718461941870
X(19)= 99.999935923870551
X(20)= 99.999996796239314

Em COBOL no Linux:
X(01)=  4.470588235294118
X(02)=  4.644736842105272
X(03)=  4.770538243626253
X(04)=  4.855700712593068
X(05)=  4.910847499165008
X(06)=  4.945537405797454
X(07)=  4.966962615594416
X(08)=  4.980046382396752
X(09)=  4.987993122733704
X(10)=  4.993044417666328
X(11)=  5.001145954388894
X(12)=  5.107165361144283
X(13)=  7.147823677868234
X(14)= 35.069409660592417
X(15)= 90.744337001124836
X(16)= 99.490073035205414
X(17)= 99.974374743980031
X(18)= 99.998718461941870
X(19)= 99.999935923870551
X(20)= 99.999996796239314

E aí migrei o programa para o Java…

public class Jgtc001 {
    public static void main(String[] args) throws Exception {
        double x0 = 4;
        double x1 = 4.25;
        double xi = 0;
        double y = 0;
        double z = 0;
        for (int i=1; i<=20; i++) {
            y = x1;
            z = x0;
            xi = 108 - ((815 - (1500 / z)) / y);
            x0 = x1;
            x1 = xi;
            System.out.println("X(" + i + ")=" + String.format("%3.15f", xi));
        }
        System.exit(0);
    }
}

…e o resultado foi um desastre:

COBOL
X(01)=  4.470588235294118
X(02)=  4.644736842105272
X(03)=  4.770538243626253
X(04)=  4.855700712593068
X(05)=  4.910847499165008
X(06)=  4.945537405797454
X(07)=  4.966962615594416
X(08)=  4.980046382396752
X(09)=  4.987993122733704
X(10)=  4.993044417666328
X(11)=  5.001145954388894
X(12)=  5.107165361144283
X(13)=  7.147823677868234
X(14)= 35.069409660592417
X(15)= 90.744337001124836
X(16)= 99.490073035205414
X(17)= 99.974374743980031
X(18)= 99.998718461941870
X(19)= 99.999935923870551
X(20)= 99.999996796239314

Java
X(1)=4.470588235294116
X(2)=4.644736842105218
X(3)=4.770538243625083
X(4)=4.855700712568563
X(5)=4.910847498660630
X(6)=4.945537395530508
X(7)=4.966962408040999
X(8)=4.980042204293014
X(9)=4.987909232795786
X(10)=4.991362641314552
X(11)=4.967455095552268
X(12)=4.429690498308830
X(13)=-7.817236578459315
X(14)=168.939167671064580
X(15)=102.039963152059270
X(16)=100.099947516249700
X(17)=100.004992040972440
X(18)=100.000249579237300
X(19)=100.000012478620160
X(20)=100.000000623921610

Repare que nos primeiros valores já existem diferenças lá nas últimas casas decimais, o que em alguns casos poderia ser até desprezível. Mas a partir do décimo cálculo as discrepâncias atingem várias ordens de grandeza, até chegar à parte inteira do resultado, o que evidentemente seria inaceitável num projeto de verdade.

Por que isso acontece?

Antes de tentar entender o que aconteceu precisamos deixar claro que não se trata de um bug do Java. O Java até conseguiria chegar ao resultado correto, mas não dessa forma, que seria a primeira opção de boa parte dos programadores envolvidos num eventual projeto de modernização.

O problema está na maneira como computadores armazenam decimais. Campos com ponto flutuante permitem que o computador armazene números muito grandes, ou muito pequenos, em apenas 32 bits (no padrão single precision) ou 64 bits (no padrão double precision). A localização do ponto decimal “flutua” em função de um expoente, mas com isso perde-se precisão. Tem um artigo muito bom que descreve esse processo e que você pode ler clicando aqui.

Se essa localização fosse fixa (como o COBOL costuma fazer), números muito grandes, ou muito pequenos, necessitariam de mais espaço, o que naturalmente exigiria mais memória, mais storage e mais tempo de processamento. Em outras palavras, campos com floating points são pequenos e rápidos, mas muito pouco precisos.

Possíveis soluções de contorno

A solução é fazer o Java trabalhar com campos fixed point, como o COBOL, e para isso existem algumas opções.

A primeira delas é substituir o tipo nativo do Java (float) por uma classe como java.math.BigDecimal. O detalhe é que quando falamos em “classe” estamos falando que haverá um “programa” (para manter a terminologia que nós coboleiros costumamos usar) para representar, armazenar e fazer contas com cada uma das variáveis desse tipo. Ou seja, overhead…

Vamos ver como ficaria nosso programa migrado com essa solução.

import java.math.BigDecimal;
import java.math.BigInteger;
import java.math.MathContext;
import java.math.RoundingMode;

public class Jgtc003 {
    public static void main(String[] args) throws Exception {

        BigDecimal x0 = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL64);
        BigDecimal x1 = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL64);
        BigDecimal xi = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL64);
        BigDecimal y = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL64);
        BigDecimal z = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL64);

        x0 = BigDecimal.valueOf(4);
        x1 = BigDecimal.valueOf(4.25);

        for (int i=1; i<=20; i++) {
            y = x1;
            z = x0;

//          xi = 108 - ((815 - (1500 / z)) / y);

            xi = BigDecimal.valueOf(1500).divide(z, 15, RoundingMode.HALF_DOWN);
            xi = BigDecimal.valueOf(815).subtract(xi);
            xi = xi.divide(y, 15, RoundingMode.HALF_DOWN);
            xi = BigDecimal.valueOf(108).subtract(xi);

            x0 = x1;
            x1 = xi;
            System.out.println("X(" + i + ")=" + xi);

        }
        System.exit(0);
    }
}

Ficou um pouco mais complicado do que a versão anterior. Tivemos que substituir as operações aritméticas nativas por métodos da classe BigDecimal, incorporar outras classes ao programa para fixar uma escala de 15 decimais para as variáveis.

E os resultados até melhoraram, como podemos ver na comparação abaixo, mais ainda está longe de ser considerado aceitável:

COBOL
X(01)=  4.470588235294118
X(02)=  4.644736842105272
X(03)=  4.770538243626253
X(04)=  4.855700712593068
X(05)=  4.910847499165008
X(06)=  4.945537405797454
X(07)=  4.966962615594416
X(08)=  4.980046382396752
X(09)=  4.987993122733704
X(10)=  4.993044417666328
X(11)=  5.001145954388894
X(12)=  5.107165361144283
X(13)=  7.147823677868234
X(14)= 35.069409660592417
X(15)= 90.744337001124836
X(16)= 99.490073035205414
X(17)= 99.974374743980031
X(18)= 99.998718461941870
X(19)= 99.999935923870551
X(20)= 99.999996796239314

JAVA
X(1)=4.470588235294118
X(2)=4.644736842105271
X(3)=4.770538243626231
X(4)=4.855700712592606
X(5)=4.910847499155498
X(6)=4.945537405603871
X(7)=4.966962611681000
X(8)=4.980046303618682
X(9)=4.987991540991751
X(10)=4.993012708353129
X(11)=5.000510934790509
X(12)=5.094480439139274
X(13)=6.904184811805049
X(14)=32.601714976939753
X(15)=89.665367518797276
X(16)=99.423777409662639
X(17)=99.971023895048601
X(18)=99.998550834929925
X(19)=99.999927542499663
X(20)=99.999996377176455

Só como comentário, o resultado é o mesmo usando MathContext.DECIMAL32, MathContext.DECIMAL64, MathContext.DECIMAL128, RoundingMode.HALF_DOWN, RoundingMode.HALF_UP ou RoudingMode.HALF_EVEN.

Ainda teríamos que quebrar muito a cabeça, talvez desenvolvendo nossas próprias classes e métodos e/ou repensar todo o processo de cálculo se esse fosse um critério do cliente para aceitar o projeto. Mas como isso é um artigo, e não um projeto, acho que podemos parar por aqui.

Se você quiser ou precisar explorar outras soluções para esse problema, existe um artigo muito bom sobre esse tema que você pode ler clicando aqui.

E o overhead?

Ficou claro nos parágrafos anteriores que a simples substituição de tipos nativos por classes não seria uma solução definitiva. Muita coisa ainda teria que ser acrescentada ao programa migrado para cravar os resultados.

Mas mesmo essa solução mais simples (e ainda inaceitável) traria um segundo problema ao nosso projeto de migração: performance.

Para avaliar o impacto, vamos modificar os programas para aumentar a profundidade do cálculo e obter os tempos de processamento no Java com tipo nativo (double) e no Java com BigDecimal.

Vamos aumentar o loop para 100 mil vezes. E como não precisamos mais comparar os resultados vou eliminar os displays intermediários:

O Java com double ficou assim:

import java.text.SimpleDateFormat;
import java.util.Date;

public class Jgtc004 {
    public static void main(String[] args) throws Exception {
        int N = 100000;
        double x0 = 4;
        double x1 = 4.25;
        double xi = 0;
        double y = 0;
        double z = 0;
        String inicio = new SimpleDateFormat("HHmmssSSS").format(new Date());
        for (int i=1; i<=N; i++) {
            y = x1;
            z = x0;
            xi = 108 - ((815 - (1500 / z)) / y);
            x0 = x1;
            x1 = xi;
        }
        String termino = new SimpleDateFormat("HHmmssSSS").format(new Date());
        System.out.println("Inicio: " + inicio + " Fim: " + termino);
        System.exit(0);
    }
}

E o Java com BigDecimal…

import java.math.BigDecimal;
import java.math.BigInteger;
import java.math.MathContext;
import java.math.RoundingMode;
import java.text.SimpleDateFormat;
import java.util.Date;

public class Jgtc005 {
    public static void main(String[] args) throws Exception {
        int N = 100000;
        BigDecimal x0 = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL32);
        BigDecimal x1 = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL32);
        BigDecimal xi = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL32);
        BigDecimal y = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL32);
        BigDecimal z = new BigDecimal(BigInteger.valueOf(0), 15, MathContext.DECIMAL32);
        x0 = BigDecimal.valueOf(4);
        x1 = BigDecimal.valueOf(4.25);
        String inicio = new SimpleDateFormat("HHmmssSSS").format(new Date());
        for (int i=1; i<=N; i++) {
            y = x1;
            z = x0;
            xi = BigDecimal.valueOf(1500).divide(z, 15, RoundingMode.HALF_UP);
            xi = BigDecimal.valueOf(815).subtract(xi);
            xi = xi.divide(y, 15, RoundingMode.HALF_UP);
            xi = BigDecimal.valueOf(108).subtract(xi);
            x0 = x1;
            x1 = xi;
        }
        String termino = new SimpleDateFormat("HHmmssSSS").format(new Date());
        System.out.println("Inicio: " + inicio + " Fim: " + termino);
        System.exit(0);
    }
}

Os tempos obtidos estão no quadro abaixo:

Java com double
Inicio: 160024185
Fim:    160024189
4 ms

Java com BigDecimal
Inicio: 160049632
Fim:    160049803
171 ms

Ou seja, com BigDecimal tivemos um tempo quase 43 vezes maior. Agora imagine isso em um sistema do mundo real, que tem que rodar numa janela pequena de produção ou dar throughput para milhares de transações simultâneas.

Conclusão

Migrar sistemas de uma plataforma para outra envolve desafios muito maiores do que a simples tradução de programas e conversão de dados, e muitos projetos desse tipo deram enormes prejuízos ou simplesmente naufragaram por causa de situações desse tipo.

Claro que existem soluções técnicas para resolver o problema de arredondamento, mas acho que consegui mostrar que não são triviais. Se você já passou por isso deixei seus comentários no fim dessa página explicando como o problema foi resolvido.

Seria esse mais um dos motivos que fazem com que o COBOL domine o mercado financeiro por tanto tempo?

Acredito que sim.